C/2020 H11 PanSTARRS-Lemmon
more info
Comet C/2020 H11 was discovered on 21 April 2020, about 5 months before its perihelion passage. Later a series of pre-discovery observations were found going ten months back to 2 June 2019. This comet was observed to 8 May 2021.
Two similar approaches to Earth took place: on 4 May 2020 (6.81 au about 3.5 months before its perihelion passage) and 4 April 2021 (6.86 au about 7.5 months after perihelion).
The preferred GR solution given here is based on data span over 1.93 yr in a range of heliocentric distances: 8.17 au – 7.63 au (perihelion) – 7.77 au.
This long-period comet entered the planetary zone having original semimajor axis of about 4,500 au and suffers small planetary perturbations during its passage through the planetary system that lead to a bit tight future orbit (semimajor axis of about 3,100 au).
Two similar approaches to Earth took place: on 4 May 2020 (6.81 au about 3.5 months before its perihelion passage) and 4 April 2021 (6.86 au about 7.5 months after perihelion).
The preferred GR solution given here is based on data span over 1.93 yr in a range of heliocentric distances: 8.17 au – 7.63 au (perihelion) – 7.77 au.
This long-period comet entered the planetary zone having original semimajor axis of about 4,500 au and suffers small planetary perturbations during its passage through the planetary system that lead to a bit tight future orbit (semimajor axis of about 3,100 au).
| solution description | ||
|---|---|---|
| number of observations | 53 | |
| data interval | 2019 06 02 – 2021 05 08 | |
| data type | perihelion within the observation arc (FULL) | |
| data arc selection | entire data set (STD) | |
| range of heliocentric distances | 8.17 au – 7.63 au (perihelion) – 7.77 au | |
| detectability of NG effects in the comet's motion | NG effects not determinable | |
| type of model of motion | GR - gravitational orbit | |
| data weighting | NO | |
| number of residuals | 101 | |
| RMS [arcseconds] | 0.21 | |
| orbit quality class | 1a | |
| previous orbit statistics, both Galactic and stellar perturbations were taken into account | ||
|---|---|---|
| no. of returning VCs in the swarm | 5001 | * |
| no. of escaping VCs in the swarm | 0 | |
| no. of hyperbolas among escaping VCs in the swarm | 0 | |
| previous reciprocal semi-major axis [10-6 au-1] | 221.18 – 224.01 – 226.82 | |
| previous perihelion distance [au] | 7.6489 – 7.65 – 7.651 | |
| previous aphelion distance [103 au] | 8.81 – 8.92 – 9.03 | |
| time interval to previous perihelion [Myr] | 0.292 – 0.298 – 0.303 | |
| percentage of VCs with qprev < 10 | 100 | |
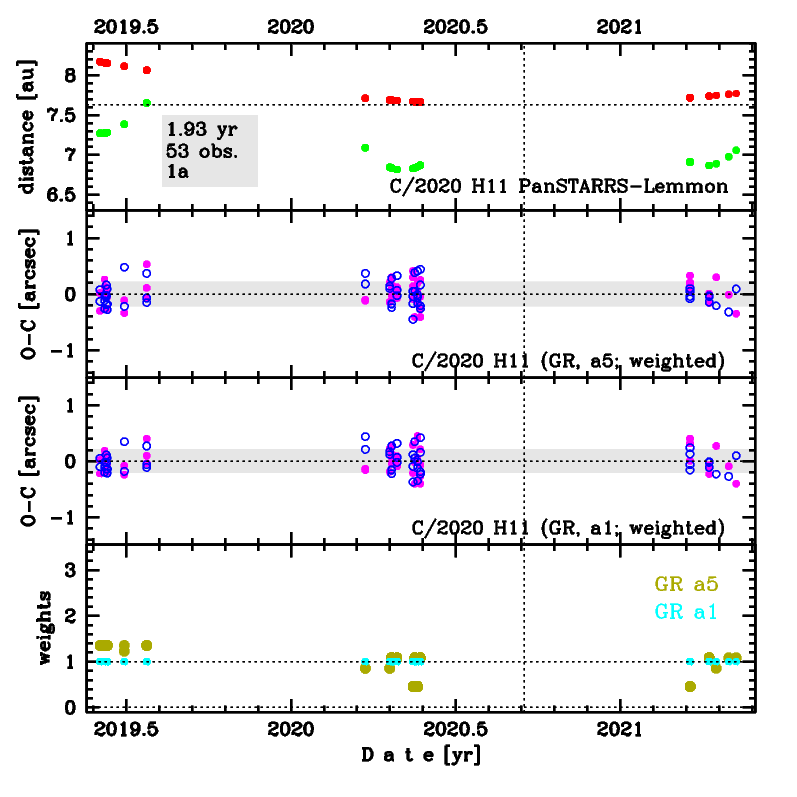
Upper panel: Time distribution of positional observations with corresponding heliocentric (red curve) and geocentric (green curve) distance at which they were taken. The horizontal dotted line shows the perihelion distance for a given comet whereas vertical dotted line — the moment of perihelion passage.
Middle panel(s): O-C diagram for a given solution (sometimes in comparison to another solution available in CODE), where residuals in right ascension are shown using magenta dots and in declination by blue open circles.
Lowest panel: Relative weights for a given data set(s).
Middle panel(s): O-C diagram for a given solution (sometimes in comparison to another solution available in CODE), where residuals in right ascension are shown using magenta dots and in declination by blue open circles.
Lowest panel: Relative weights for a given data set(s).
| previous_g orbit statistics, here only the Galactic tide has been included | ||
|---|---|---|
| no. of returning VCs in the swarm | 5001 | * |
| no. of escaping VCs in the swarm | 0 | |
| no. of hyperbolas among escaping VCs in the swarm | 0 | |
| previous reciprocal semi-major axis [10-6 au-1] | 221.18 – 224.01 – 226.81 | |
| previous perihelion distance [au] | 7.6502 – 7.6513 – 7.6524 | |
| previous aphelion distance [103 au] | 8.81 – 8.92 – 9.03 | |
| time interval to previous perihelion [Myr] | 0.292 – 0.298 – 0.304 | |
| percentage of VCs with qprev < 10 | 100 | |